Are you a Queensland high school student gearing up for your QCE Specialist Mathematics exam? Look no further! This comprehensive guide is designed to help you ace your exam and secure that coveted A grade. Whether you're struggling with complex mathematical concepts or simply looking to refine your exam strategy, we've got you covered.

Specialist Mathematics is known for its challenging content and rigorous assessment, but with the right preparation and mindset, success is within your reach. In this blog post, we'll walk you through everything you need to know about the QCE Specialist Mathematics exam, including:

1. A summary of the units covered in the curriculum
2. The format and structure of the exam
3. Effective revision strategies tailored for Specialist Mathematics
4. Access to past papers and practice resources
5. Why past papers are crucial for your exam preparation
6. Tips for the week leading up to the exam and exam day itself

By the end of this guide, you'll be equipped with the knowledge and confidence to tackle even the most challenging questions in your QCE Specialist Mathematics exam. Let's dive in and set you on the path to achieving that A grade!

Summary of Units

Below we will cover Units 3 and 4 in Specialist Mathematics and all the sub-topics you will need to understand to do well on your Specialist Mathematics exam:

Unit 3: Further complex numbers, proof, vectors and

matrices

Topic 1: Further complex numbers

Complex arithmetic using polar form (3 hours)

Roots of complex numbers (3 hours)

• Determine and examine the th roots of unity and their location on the unit circle.
• Determine and examine the th roots of complex numbers and their location in the complexplane.

Factorisation of polynomials (5 hours)

• Apply the factor theorem and the remainder theorem for polynomials.
• Understand and use the complex conjugate root theorem for polynomials with real coefficients
  e.g. factorise a cubic polynomial with real coefficients given one factor.
• Solve polynomial equations over to order 4 including those with real and imaginary coefficients

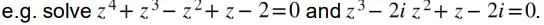
Topic 2: Mathematical induction and trigonometric proofs

Mathematical induction (8 hours)

Trigonometric proofs using De Moivre’s theorem (2 hours)

Topic 3: Vectors in two and three dimensions

Vectors in three dimensions (3 hours)

Algebra of vectors in three dimensions (3 hours)

• Examine and use addition and subtraction of vectors in Cartesian form.
• Use multiplication by a scalar of a vector in Cartesian form.
• Determine a vector between two points.
• Use a vector representing a section of a line segment, including the midpoint of a line segment.
• Use the scalar (dot) product.

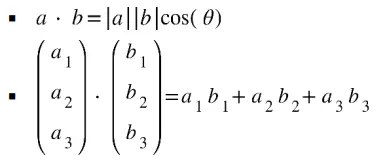
• Examine properties of parallel and perpendicular vectors and determine if two vectors areparallel or perpendicular.
• Use scalar and vector projections of vectors

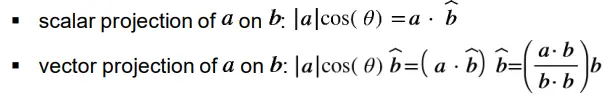
• Apply the scalar product to vectors expressed in Cartesian form.
• Model and solve problems that involve displacement, force, velocity and relative velocity usingthe above concepts.
• Use vectors to prove geometric results in two dimensions (other than those listed in Unit 2Topic 3) and in three dimensions.

Vector and Cartesian equations (7 hours)

• Understand and use equations of spheres

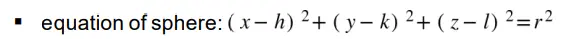
• Use vector equations of curves in two or three dimensions involving a parameter, and determine a ‘corresponding’ Cartesian equation in the two-dimensional case.
• Determine vector, parametric and Cartesian equations of straight lines and straight-line segments given the position of two points, or equivalent information, in both two and three dimensions.

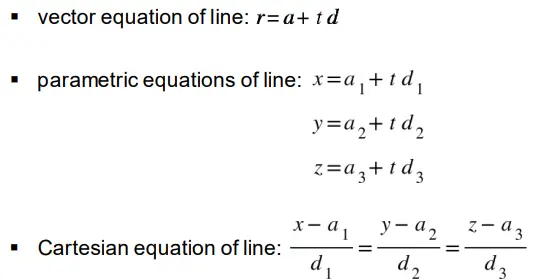
• Define and use the vector (cross) product to determine a vector normal to a given plane, with and without technology.

• Use vector methods in applications, including areas of shapes and determining vector and Cartesian equations of a plane and of regions in a plane.

Topic 4: Vector calculus

Vector calculus (9 hours)

• Understand and use position of vectors as a function of time.
• Understand and use the Cartesian equation of a path given as a vector equation in two dimensions, including circles, ellipses and hyperbolas.

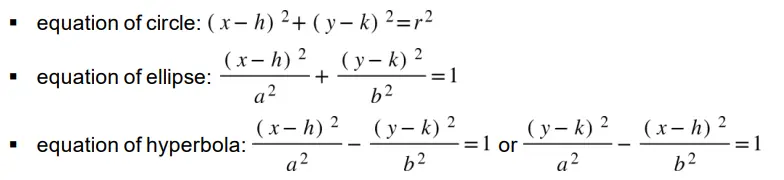
• Understand and use the position of two particles, each described as a vector function of time,and determine if their paths cross or if the particles meet.
• Differentiate and integrate a vector function with respect to time.
• Use vector calculus to determine equations of motion of a particle travelling in a straight line with both constant and variable acceleration.
• Apply vector calculus to model and solve problems that involve motion in a plane, including projectile and circular motion, with and without technology.

Topic 5: Further matrices

Matrix algebra and systems of equations (5 hours)

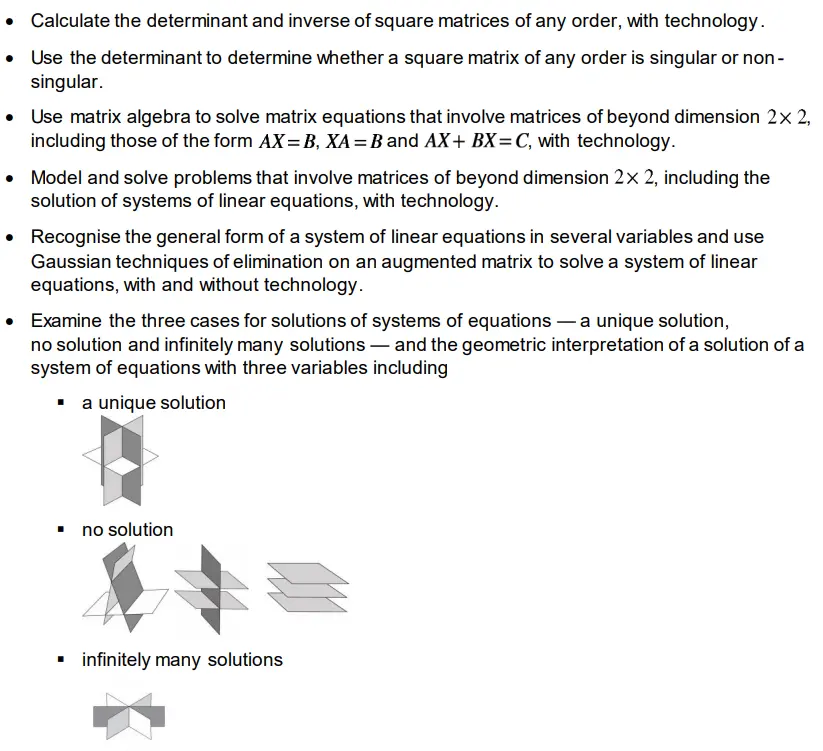
Applications of matrices (7 hours)

• Model and solve problems that involve real-life situations using matrices, including Dominancea nd Leslie matrices.
• Investigate how matrices have been applied in other real-life situations, e.g. Leontief, Markov,area, cryptology, eigenvectors and eigenvalues.

‍

📌 Note: The external examination may assess only Dominance and Leslie matrices.

‍

Unit 4: Further calculus and statistical inference

Topic 1: Integration techniques

Integration techniques (10 hours(

Topic 2: Applications of integral calculus

Applications of integral calculus (10 hours)

• Apply techniques from Unit 4 Topic 1 Sub-topic: Integration techniques to calculate areas between curves determined by functions, with and without technology.
• Determine volumes of solids of revolution about either axis, with and without technology.

• Use Simpson’s rule to approximate an area and the value of a definite integral, with and without technology.

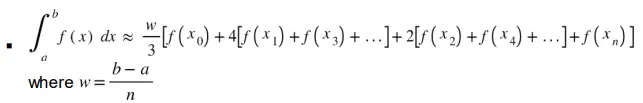
Topic 3: Rates of change and differential equations

Rates of change (3 hours)

• Use implicit differentiation to determine the gradient of curves whose equations are given in implicit form.
• Model and solve related rates problems as instances of the chain rule including situations that involve surface area and volume of cones, pyramids and spheres, with and withouttechnology.

Differential equations (8 hours)

Topic 4: Modelling motion

Modelling motion (11 hours)

Topic 5: Statistical inference

Sample means (7 hours)

Confidence intervals for means (6 hours)

source: Specialist Mathematics 2025 v1.0: General senior syllabus

Format of the Exam

Understanding the structure and format of the QCE Specialist Mathematics exam is crucial for effective preparation. The Queensland Curriculum and Assessment Authority (QCAA) has designed the exam to thoroughly assess your knowledge and skills across all units. Let's break down what you can expect on exam day:

Overall Structure

The QCE Specialist Mathematics external assessment consists of two papers:

1. Paper 1: Technology-free exam
2. Paper 2: Technology-active exam

Both papers are equally weighted, each contributing 50% to your final external assessment result.

Paper 1: Technology-free Exam

• Duration: 2 hours plus 15 minutes perusal time
• Questions: Short response questions
• Topics Covered: All units (1-4)
• Marks: 100 marks

Key points about Paper 1:

• No calculators or technology allowed
• Focus on analytical skills and mathematical reasoning
• May include proofs, algebraic manipulations, and conceptual questions

Paper 2: Technology-active Exam

• Duration: 2 hours plus 15 minutes perusal time
• Questions: Mix of short response and extended response questions
• Topics Covered: All units (1-4)
• Marks: 100 marks

Key points about Paper 2:

• Approved graphics calculator permitted
• Emphasis on problem-solving and application of mathematical concepts
• May include data analysis, complex calculations, and modelling tasks

Question Types

In both papers, you can expect to encounter a variety of question types:

1. Short Answer Questions: These require brief responses, often involving calculations or explanations.
2. Extended Response Questions: These require longer, more detailed answers, often involving multiple steps or concepts.
3. Interpretation Questions: You may be asked to interpret graphs, diagrams, or data sets.
4. Proof Questions: Especially in Paper 1, you might need to construct mathematical proofs.
5. Application Questions: These involve applying mathematical concepts to real-world scenarios.

‍

💡 Take notes efficiently and effectively using these tips!

‍

‍

Marking Criteria

The QCAA uses the following criteria to assess your performance:

• Accuracy: Correctness of calculations and answers
• Procedural Fluency: Efficiency and appropriateness of methods used
• Problem-solving: Ability to interpret, model, and solve complex problems
• Communication: Clarity and precision in mathematical explanations and reasoning

Tips for Navigating the Exam Format

1. Time Management: Allocate your time wisely between questions. A rough guide is about 1 minute per mark.
2. Show Your Work: Even if using a calculator in Paper 2, show your working out. You can earn partial marks even if the final answer is incorrect.
3. Practice Both Styles: Ensure you're comfortable solving problems both with and without technology.
4. Read Carefully: Use the perusal time to read through all questions and plan your approach.
5. Tackle Easier Questions First: Build confidence by answering questions you're sure about before moving to more challenging ones.

Understanding the exam format is half the battle. By familiarising yourself with the structure and expectations of both papers, you'll be better prepared to showcase your mathematical skills and knowledge on exam day.

‍

Specific Study Advice for QCE Specialist Mathematics Exam

Given the unique structure and challenging nature of the QCE Specialist Mathematics exam, here's some targeted advice to help you prepare effectively:

1. Master Both Technology-Free and Technology-Active Techniques

Remember, the exam consists of two equally weighted papers:

• Paper 1 (Technology-free): Practice solving complex problems without a calculator. Focus on:
  • Algebraic manipulations
  • Proving mathematical statements
  • Mental calculation strategies
  • Sketch graphs by hand
• Paper 2 (Technology-active): Become proficient with your approved graphics calculator. Practice:
  • Complex calculations
  • Data analysis
  • Graphing functions
  • Solving equations numerically

2. Develop Problem-Solving Skills for Extended Response Questions

The exam, especially Paper 2, includes extended response questions. To excel in these:

• Practice breaking down complex problems into manageable steps
• Learn to clearly communicate your mathematical reasoning
• Develop strategies for problems that combine multiple topic areas

3. Understand the Cognitive Verbs

QCE exams use specific cognitive verbs in questions. Familiarise yourself with terms like:

• Analyse
• Evaluate
• Justify
• Prove
• Synthesise

Understand what each verb requires in your response.

4. Time Management Strategies

With 2 hours for each paper (plus 15 minutes perusal time), time management is crucial:

• Use the perusal time to read through all questions and plan your approach
• Allocate roughly 1 minute per mark as a general guide
• Practice completing full exams under timed conditions

5. Utilise QCAA Resources

The QCAA provides valuable resources specific to the QCE Specialist Mathematics exam:

• Study the sample assessments available on the QCAA website
• Review the syllabus to understand the depth required for each topic
• Use the formula sheet provided by QCAA in your practice sessions

6. Focus on Understanding, Not Just Memorisation

The QCE Specialist Mathematics exam tests deep understanding:

• Practice applying concepts to unfamiliar contexts
• Understand the connections between different mathematical areas
• Be prepared to use knowledge from General Mathematics and Mathematical Methods

7. Prepare for the Cognitive Demands

QCE Specialist Mathematics questions often require high-order thinking:

• Practice questions that require you to analyse, evaluate, and create
• Develop skills in mathematical modelling and problem-solving
• Be prepared to apply mathematical concepts to real-world scenarios

By focusing your study on these specific aspects of the QCE Specialist Mathematics exam, you'll be well-prepared to tackle both the technology-free and technology-active papers, and to demonstrate your mathematical skills across all required topic areas.

Link to past papers:

‍

Why Past Papers are the Best Way to Revise for QCE Specialist Mathematics

When it comes to preparing for your QCE Specialist Mathematics exam, past papers are an invaluable resource. Here's why they should be a cornerstone of your revision strategy:

1. Familiarisation with QCE Question Structure

• Consistent Format: QCE Specialist Mathematics exams tend to use consistent question structures. These can differ significantly from exercises in textbooks or other resources.
• Two-Paper Format: Past papers help you practice for both the technology-free (Paper 1) and technology-active (Paper 2) components of the exam.
• Question Types: You'll become familiar with the mix of short response and extended response questions typical in QCE exams.

2. Rapid Identification of Challenging Areas

• Topic-Specific Difficulties: Quickly pinpoint which mathematical concepts or topics you find most challenging.
• Question Style Challenges: Identify if you struggle more with theoretical questions (common in Paper 1) or applied problems (often in Paper 2).
• Targeted Revision: Focus your study efforts on areas where you consistently lose marks.

3. Time Management Practice

• Realistic Timing: Practice allocating your time effectively across the 2-hour duration of each paper.
• Identify Time Pressure Points: Recognise which types of questions or topics require more time for you to complete.
• Perusal Time Strategy: Learn to use the 15-minute perusal time effectively to plan your approach.

4. Exposure to QCE-Specific Mathematical Language

• Cognitive Verbs: Familiarise yourself with QCE-specific terms like "analyse," "evaluate," and "justify" in a mathematical context.
• Question Interpretation: Improve your ability to extract relevant information from complex word problems.

5. Practice with Integrated Topics

• Cross-Unit Questions: QCE Specialist Mathematics often includes questions that integrate concepts from multiple units.
• Synoptic Thinking: Develop the ability to connect different areas of mathematics, a key skill for success in this exam.

6. Calculator and Non-Calculator Skills

• Balanced Practice: Alternate between Papers 1 and 2 to maintain proficiency in both manual calculation and technology-aided problem-solving.
• Graphics Calculator Mastery: Become adept at using your approved calculator for complex calculations and graphing in Paper 2.

7. Exam Technique Refinement

• Working Out Presentation: Learn how to present your solutions clearly, which is crucial for scoring full marks.
• Multi-Step Problem Strategy: Develop strategies for breaking down complex, multi-step problems common in Specialist Mathematics.

8. Confidence Building

• Familiarity Breeds Confidence: Regular practice with past papers reduces exam anxiety by making the format feel routine.
• Progress Tracking: Seeing improvement in your scores over time boosts confidence in your abilities.

Caution Note:

While past papers are extremely valuable, it's important to use them wisely:

• Syllabus Changes: Be aware that the QCE Specialist Mathematics syllabus may change over time. Questions from older papers might cover topics that are no longer part of the current curriculum.
• Evolving Question Styles: The style and complexity of questions may evolve. Always refer to the most recent QCAA guidelines and sample assessments.
• Supplement with Current Resources: Combine past paper practice with up-to-date textbooks and QCAA-approved resources to ensure comprehensive coverage of the current syllabus.

By making past papers a key part of your revision strategy, you'll not only improve your mathematical skills but also develop the exam-specific techniques needed to excel in QCE Specialist Mathematics. Remember, the goal is not just to memorise solutions, but to understand the underlying concepts and problem-solving strategies that these papers help you practice.

‍

Final Preparation Tips for QCE Specialist Mathematics Exam

As your QCE Specialist Mathematics exam approaches, it's crucial to fine-tune your preparation and manage your mindset. Here are some specific tips for the week before, the night before, and the day of your exam:

Week Before the Exam

1. Review Key Concepts:
   • Focus on major topics like vectors, complex numbers, and calculus applications.
   • Pay special attention to integration techniques and differential equations.
2. Practice with Past Papers:
   • Complete at least one full practice exam under timed conditions for both Paper 1 and Paper 2.
   • Review your performance, focusing on time management and areas of weakness.
3. Memorise Essential Formulas:
   • While a formula sheet is provided, memorise key formulas for efficiency.
   • Focus on trigonometric identities, vector operations, and integration rules.
4. Graphics Calculator Check:
   • Ensure your approved calculator is in good working order.
   • Practice complex calculations and graphing functions you might need in Paper 2.
5. Review Cognitive Verbs:
   • Refresh your understanding of QCE-specific terms like "analyse," "evaluate," and "justify."
   • Practice interpreting these in the context of mathematical problems.

💡 Check out these effective study techniques to ace your exam!

Night Before the Exam

1. Light Review:
   • Briefly go over summary notes, focusing on areas you find challenging.
   • Review the structure of both Paper 1 (technology-free) and Paper 2 (technology-active).
2. Prepare Your Materials:
   • Pack your approved calculator, spare batteries, and necessary stationery.
   • Double-check the exam time and location.
3. Relaxation Techniques:
   • Practice deep breathing or light stretching to manage exam anxiety.
   • Avoid last-minute cramming, which can increase stress levels.
4. Early Bedtime:
   • Aim for at least 8 hours of sleep to ensure you're well-rested for the exam.

Day of the Exam

Healthy Breakfast:

1. Eat a balanced meal to maintain energy levels throughout the exam.
2. Stay hydrated, but avoid excessive caffeine.

Arrival Time:

1. Aim to arrive at the exam venue at least 30 minutes early.
2. Use this time to calm your nerves and focus your thoughts.

Warm-Up Exercises:

1. Do a few simple calculations to get your mind into "math mode."
2. Review key formulas one last time, especially for Paper 1 where you won't have calculator assistance.

Exam Strategy:

For Paper 1 (Technology-free):

• Use the perusal time to identify question types and plan your approach.
• Start with questions you're confident about to build momentum.
• Show all working clearly, as partial marks are often available.

For Paper 2 (Technology-active):

• Quickly check your calculator is functioning correctly.
• For complex calculations, write down the steps you input into your calculator.
• Use your calculator efficiently for graphing and solving equations.
  

Time Management:

1. Allocate roughly 1 minute per mark as a general guide.
2. If stuck on a question, make a note and move on - you can return to it if time allows.

Answer All Questions:

1. Even if unsure, attempt every question. Partial marks can add up significantly.

Check Your Work:

1. If time allows, review your answers, especially for calculation-heavy questions.

Stay Calm:

1. If you encounter a difficult question, take a deep breath and approach it step-by-step.
2. Remember, it's normal to find some questions challenging - stay focused and do your best.

Remember, your QCE Specialist Mathematics exam is a chance to showcase the skills and knowledge you've developed. Stay confident, trust in your preparation, and approach each question methodically. Good luck!